Поляризацията е една от основните характеристики на антените. Първо трябва да разберем поляризацията на плоските вълни. След това можем да обсъдим основните видове поляризация на антените.
линейна поляризация
Ще започнем да разбираме поляризацията на плоска електромагнитна вълна.
Планарната електромагнитна (ЕМ) вълна има няколко характеристики. Първата е, че мощността се разпространява в една посока (полето не се променя в две ортогонални посоки). Второ, електрическото поле и магнитното поле са перпендикулярни едно на друго и ортогонални едно на друго. Електрическите и магнитните полета са перпендикулярни на посоката на разпространение на плоската вълна. Като пример, разгледайте едночестотно електрическо поле (Е поле), дадено от уравнение (1). Електромагнитното поле се разпространява в посока +z. Електрическото поле е насочено в посока +x. Магнитното поле е в посока +y.
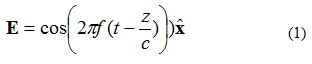
В уравнение (1) спазвайте означението: . Това е единичен вектор (вектор с дължина), който показва, че точката на електрическото поле е в посока x. Плоската вълна е илюстрирана на Фигура 1.
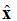
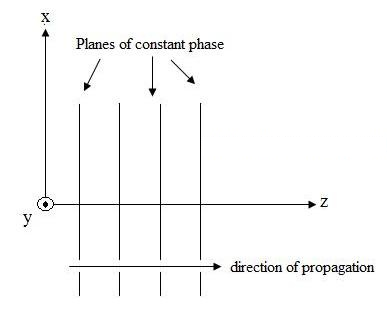
фигура 1. Графично представяне на електрическото поле, движещо се в посока +z.
Поляризацията е формата на следата и разпространението (контурата) на електрическо поле. Като пример, разгледайте уравнението (1) на електрическото поле на плоската вълна. Ще наблюдаваме позицията, където електрическото поле е (X,Y,Z) = (0,0,0) като функция на времето. Амплитудата на това поле е изобразена на Фигура 2 в няколко момента във времето. Полето осцилира с честота "F".
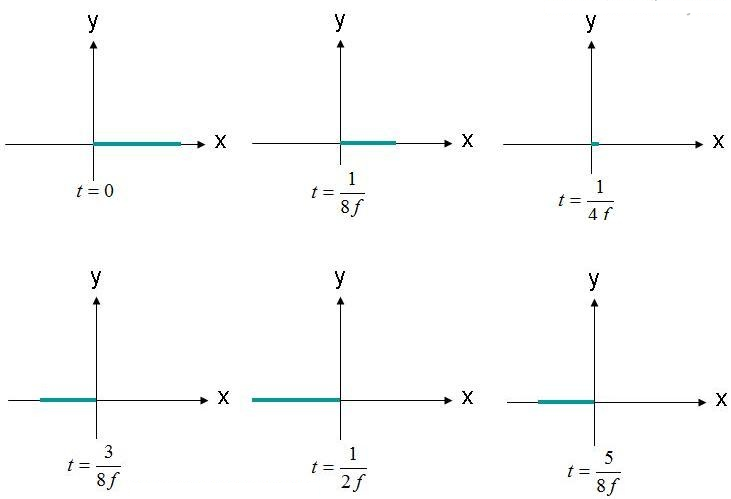
фигура 2. Наблюдавайте електрическото поле (X, Y, Z) = (0,0,0) в различни моменти от времето.
Електрическото поле се наблюдава в началото на координатната система, като осцилира напред-назад по амплитуда. Електрическото поле винаги е по протежение на посочената ос x. Тъй като електрическото поле се поддържа по една линия, може да се каже, че това поле е линейно поляризирано. Освен това, ако оста X е успоредна на земята, това поле също се описва като хоризонтално поляризирано. Ако полето е ориентирано по оста Y, може да се каже, че вълната е вертикално поляризирана.
Линейно поляризираните вълни не е необходимо да бъдат насочени по хоризонтална или вертикална ос. Например, вълна на електрическо поле с ограничение, разположено по линия, както е показано на Фигура 3, също би била линейно поляризирана.
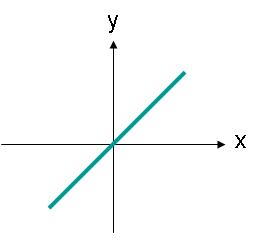
изображение 3. Амплитудата на електрическото поле на линейно поляризирана вълна, чиято траектория е ъгъл.
Електрическото поле на Фигура 3 може да бъде описано с уравнение (2). Сега има x и y компонент на електрическото поле. И двата компонента са с еднакъв размер.
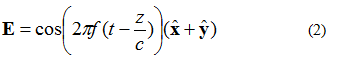
Едно нещо, което трябва да се отбележи относно уравнение (2), е xy-компонентата и електронните полета във втория етап. Това означава, че и двата компонента имат еднаква амплитуда по всяко време.
кръгова поляризация
Сега да приемем, че електрическото поле на плоска вълна е дадено от уравнение (3):
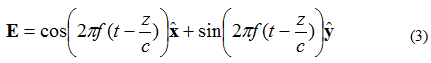
В този случай, X- и Y-елементите са 90 градуса извън фаза. Ако полето се наблюдава като (X, Y, Z) = (0,0,0) отново, както преди, кривата на електрическото поле спрямо времето ще изглежда, както е показано по-долу на Фигура 4.
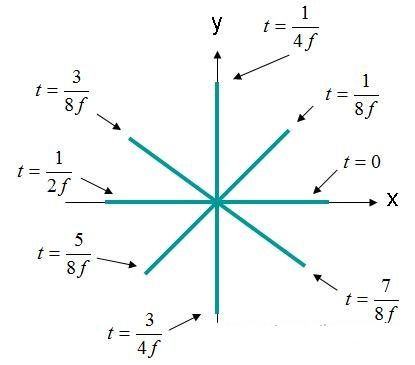
Фигура 4. Силата на електрическото поле (X, Y, Z) = (0,0,0) EQ домейн. (3).
Електрическото поле на Фигура 4 се върти в кръг. Този тип поле се описва като кръгово поляризирана вълна. За кръгова поляризация трябва да бъдат изпълнени следните критерии:
- Стандарт за кръгова поляризация
- Електрическото поле трябва да има два ортогонални (перпендикулярни) компонента.
- Ортогоналните компоненти на електрическото поле трябва да имат еднакви амплитуди.
- Квадратурните компоненти трябва да са извън фаза на 90 градуса.
Ако се движи по екрана на Вълнова Фигура 4, се казва, че въртенето на полето е обратно на часовниковата стрелка и е с дясна кръгова поляризация (RHCP). Ако полето се върти по посока на часовниковата стрелка, то ще бъде с лява кръгова поляризация (LHCP).
Елиптична поляризация
Ако електрическото поле има два перпендикулярни компонента, разположени на 90 градуса извън фазата, но с еднаква величина, полето ще бъде елиптично поляризирано. Като се има предвид електрическото поле на плоска вълна, движеща се в посока +z, описана от уравнение (4):
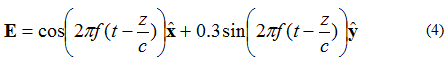
Местоположението на точката, в която ще се намира върхът на вектора на електрическото поле, е показано на Фигура 5
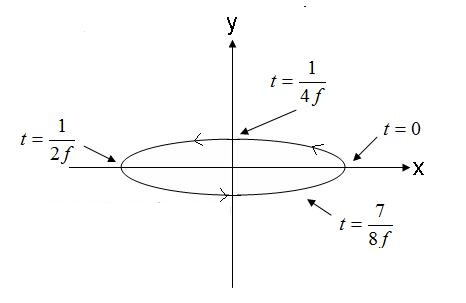
Фигура 5. Електрическо поле на вълна с елиптична поляризация. (4).
Полето на Фигура 5, движещо се обратно на часовниковата стрелка, би било дясно-елиптично, ако се движи извън екрана. Ако векторът на електрическото поле се върти в обратна посока, полето ще бъде ляво-елиптично поляризирано.
Освен това, елиптичната поляризация се отнася до нейната ексцентричност. Съотношението на ексцентричността към амплитудата на главната и второстепенната ос. Например, ексцентричността на вълната от уравнение (4) е 1/0,3 = 3,33. Елиптично поляризираните вълни се описват допълнително от посоката на главната ос. Вълновото уравнение (4) има ос, състояща се предимно от оста x. Обърнете внимание, че главната ос може да бъде под произволен ъгъл в равнината. Ъгълът не е необходим, за да пасва на оста X, Y или Z. Накрая, важно е да се отбележи, че както кръговата, така и линейната поляризация са специални случаи на елиптична поляризация. 1,0 ексцентрична елиптично поляризирана вълна е кръгово поляризирана вълна. Елиптично поляризирани вълни с безкраен ексцентричност. Линейно поляризирани вълни.
Поляризация на антената
Сега, след като сме запознати с електромагнитните полета на поляризираните равнинни вълни, поляризацията на антената е просто дефинирана.
Поляризация на антената - оценка на далечното поле на антената, поляризацията на полученото излъчено поле. Поради това антените често се обозначават като „линейно поляризирани“ или „дяснополяризирани кръгово поляризирани антени“.
Тази проста концепция е важна за антенните комуникации. Първо, хоризонтално поляризирана антена няма да комуникира с вертикално поляризирана антена. Поради теоремата за реципрочност, антената предава и приема по абсолютно един и същи начин. Следователно, вертикално поляризираните антени предават и приемат вертикално поляризирани полета. Следователно, ако се опитате да прехвърлите вертикално поляризирана хоризонтално поляризирана антена, няма да има приемане.
В общия случай, за две линейно поляризирани антени, завъртени една спрямо друга на ъгъл ( ), загубата на мощност, дължаща се на това несъответствие на поляризацията, ще бъде описана от коефициента на поляризационни загуби (PLF):
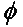
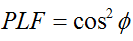
Следователно, ако две антени имат еднаква поляризация, ъгълът между техните излъчващи електронни полета е нула и няма загуба на мощност поради несъответствие в поляризацията. Ако едната антена е вертикално поляризирана, а другата е хоризонтално поляризирана, ъгълът е 90 градуса и няма да се предава мощност.
ЗАБЕЛЕЖКА: Преместването на телефона над главата ви под различни ъгли обяснява защо понякога приемането може да се подобри. Антените на мобилните телефони обикновено са линейно поляризирани, така че завъртането на телефона често може да съответства на поляризацията му, като по този начин подобрява приемането.
Кръговата поляризация е желана характеристика на много антени. И двете антени са кръгово поляризирани и не страдат от загуба на сигнал поради несъответствие в поляризацията. Антените, използвани в GPS системите, са с дясна кръгова поляризация.
Сега да предположим, че линейно поляризирана антена приема кръгово поляризирани вълни. Еквивалентно, да предположим, че кръгово поляризирана антена се опитва да приема линейно поляризирани вълни. Какъв е полученият коефициент на загуба на поляризация?
Припомнете си, че кръговата поляризация всъщност представлява две ортогонални линейно поляризирани вълни, разположени на 90 градуса извън фазата. Следователно, линейно поляризирана (LP) антена ще приема само фазовия компонент на кръгово поляризираната (CP) вълна. Следователно, LP антената ще има загуба на поляризационно несъответствие от 0,5 (-3dB). Това е вярно, независимо от ъгъла, под който е завъртяна LP антената. следователно:
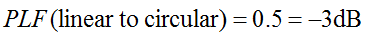
Коефициентът на загуба на поляризация понякога се нарича ефективност на поляризация, фактор на несъответствие на антената или фактор на приемане на антената. Всички тези имена се отнасят до едно и също понятие.
Време на публикуване: 22 декември 2023 г.







